This page is divided into the following sections:
Encoding a Coxeter graph / encoding a Coxeter group
The Coxeter group acting on a n-dimensional space is specified by giving its Coxeter graph or Coxeter diagram with d vertices. In order to name its vertices, you have the following two possibilities:
- use integers between 1 and d
- use custom labels: the name of each vertex can contain letters, digits, - and _ (but no space)
The graph is written in a file as follows:
- First line [mandatory]: d, n
Where d is the number of vertices of the graph and n is the dimension.
Remark: The dimension is optional (see remark below).
- Second line [optional]: name of the vertices
Remark: If this line is omitted, CoxIter will assume that the vertices are labelled with integers from 1 to d. If this line is specified, the format is the following: vertices labels: label1 label2 label3 ...
- Following lines: vertex1 vertex2 weight
Remarks:
- 0 is used to specifiy the weight infinity and 1 is used to specifiy a dotted edge
- Only one line per edge is sufficient
- The weight 2 doesn't have to be specified.
Remark about the dimension
If the dimension is not specified in the first line but is needed for the computations (for example for the compacity or finite volume tests), then CoxIter will determine the dimension by looking at the maximal spherical and euclidean graphs. In order to succeed, it is important that the associated polyhedron contains at least one vertex. Therefore, if you don't know this, try to specify the dimension.
Example
The group F4 can be encoded as follows:
It can also be encoded as follows:
4
vertices labels: t s1 s2 s3
t s1 3
s1 s2 4
s2 s3 3
Parameters of CoxIter
Mandatory parameters
- Parameters
-
| -i | Path to the file which encodes the Coxeter graph.
Example: -i graphs/graph.coxiter |
Basic optional parameters
- Parameters
-
| -full | If specified, do almost all the possible computations (except the arithmeticity test):
- Euler characteristic
- f-vector
- Finite volume test
- Compacity test
- Growth series
- Growth rate (if the PARI library is avaliable)
|
| -arithmeticity | If specified, the arithmeticity is tested.
Alias: -a
Remarks:
- The group has to be non-cocompact.
- If the graph contains dotted lines, more tests might be needed (see Example 2).
|
| -compactness | If specified, CoxIter will test the cocompactness.
Aliases: -c, -compact, -compacity, -cocompact |
| -debug | If specified, the following information will be displayed
- List of the connected euclidean graphs found
- List of the connected spherical graphs found
- List of the products of euclidean graphs (with their multiplicities)
- List of the products of spherical graphs (with their multiplicities)
Remarks:
- If -compactness is given and if the group is not cocompact, the graph which cannot be extended correctly
- If -fv is given and if the group is not of finite covolume, the graph which cannot be extended correctly
Since the output can be huge with this flag, it is suggested to also use -o and -of
|
| -fv | If specified, CoxIter will test whether the group is of finite covolume or not.
Alias: -fcv |
| -g | If specified, CoxIter will compute the growth series.
Aliases: -growth, -poincarre |
| -growthrate | If specified and if the PARI library is avaliable, CoxIter will compute the growth rate.
|
Advanced parameters
- Parameters
-
| -drawgraph | If specified, the Coxeter graph will be written
Alias: -dg
Require: -o
Remark: does not work on Windows.
Remark: see example below. |
| -drop | Label(s) of the vertex(vertices) to drop.
With this option, CoxIter will work on a subgraph of the encoded graph.
Example: use "-drop 3 -drop s2" to discard vertices 3 and s2 (and all edges starting from these vertices). |
| -o | Base name for the output
Example: "-o graphs/graph" will create files "graphs/graph.output" and "graphs/graph.jpg" |
| -of | If specified, the output of the program is written in a file (the parameter -o must be given)
Alias: -cf
Example: by specifying "-cf -o graphs/graph" the output is written in "graphs/graph.output" |
| -oformat | Format for mathematical output
Possible values are: generic, gap, latex, mathematica, pari
Example: "-pgm -oformat mathematica" will print the Gram matrix in the Mathematica format
Alias: -outputformat
Default: generic |
| -pcg | If specified, the Coxeter graph will be printed
For each vertex, a list of its neighbours is displayed |
| -pgm | If specified, the Gram matrix will be displayed
Remark: If the graph contains dotted edges, some variables will be added
See: -orformat |
| -writegraph | If specified, the graph will be written to be used in CoxIter
Alias: -wg
Require: -o
Example: by specifying "-wg -o graphs/graph" the output is written in "graphs/graph.coxiter"
Remark: You can combine this option with -drop and -drawgraph to draw a subgraph of an encoded graph.
|
Technical parameters
- Parameters
-
| -nc | If specified, some computations won't be done; they will be displayed to be given to a special software (Maxima, Mathematica, ...)
This parameter can be used in order to avoid the use of libraries BigInt and Rational_Numbers in CoxIter. |
| -nopenmp | If specified, OpenMP (parallel computations) is disabled
Alias: -nparallel
Use this if you call CoxIter from a parallelized program. |
Examples
Example 1
We want to compute the invariants of the cocompact hyperbolic Coxeter group B8 in H8 found by Bugaenko.
We create in the folder "/CoxIter/graphs/" a file named "8-Bugaenko.coxiter" which contains the description of the graph (the 1 is for the dotted line):
11 8
1 2 5
2 3 3
3 4 3
4 5 3
5 6 3
6 7 3
7 8 3
8 9 5
4 10 3
6 11 3
10 11 1
We call CoxIter:
./coxiter -i ../graphs/8-Bugaenko.coxiter -full -o ../graphs/8-Bugaenko -dg
The output is the following
Reading file: ../graphs/cocompact/8-Bugaenko.coxiter
Number of vertices: 11
Dimension: 8
Vertices: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Removed vertices:
Field generated by the entries of the Gram matrix: ?
File read
GraphViz command:
dot -Tjpg -o"../graphs/8-Bugaenko.jpg" "../graphs/8-Bugaenko.graphviz"
Finding connected subgraphs......
Finding graphs products......
Computations......
Computation time: 0.00451964s
Cocompact: yes
Finite covolume: yes
f-vector: (41, 164, 316, 374, 294, 156, 54, 11, 1)
Number of vertices at infinity: 0
Alternating sum of the components of the f-vector: 0
Euler characteristic: 24187/8709120000
Covolume: pi^4 * 24187/57153600000
Growth series:
f(x) = C(2,2,2,2,2,2,2,2,3,3,3,3,4,4,4,4,5,5,5,5,6,6,6,6,7,8,8,9,10,10,10,10,12,12,14,15,15,18,20,20,24,30,30)/(1 - 3 * x + 2 * x^2 - 3 * x^3 + 5 * x^4 - 5 * x^5 + 7 * x^6 - 11 * x^7 + 16 * x^8 - 16 * x^9 + 29 * x^10 - 31 * x^11 + 45 * x^12 - 53 * x^13 + 77 * x^14 - 80 * x^15 + 112 * x^16 - 132 * x^17 + 167 * x^18 - 200 * x^19 + 251 * x^20 - 303 * x^21 + 352 * x^22 - 445 * x^23 + 497 * x^24 - 630 * x^25 + 685 * x^26 - 884 * x^27 + 925 * x^28 - 1205 * x^29 + 1247 * x^30 - 1616 * x^31 + 1643 * x^32 - 2131 * x^33 + 2142 * x^34 - 2741 * x^35 + 2755 * x^36 - 3493 * x^37 + 3494 * x^38 - 4366 * x^39 + 4392 * x^40 - 5378 * x^41 + 5433 * x^42 - 6551 * x^43 + 6652 * x^44 - 7840 * x^45 + 8047 * x^46 - 9289 * x^47 + 9600 * x^48 - 10872 * x^49 + 11356 * x^50 - 12552 * x^51 + 13248 * x^52 - 14367 * x^53 + 15285 * x^54 - 16228 * x^55 + 17462 * x^56 - 18147 * x^57 + 19683 * x^58 - 20106 * x^59 + 21992 * x^60 - 22015 * x^61 + 24289 * x^62 - 23906 * x^63 + 26514 * x^64 - 25698 * x^65 + 28690 * x^66 - 27344 * x^67 + 30666 * x^68 - 28872 * x^69 + 32452 * x^70 - 30168 * x^71 + 34028 * x^72 - 31253 * x^73 + 35235 * x^74 - 32110 * x^75 + 36174 * x^76 - 32655 * x^77 + 36748 * x^78 - 32961 * x^79 + 36898 * x^80 - 32961 * x^81 + 36748 * x^82 - 32655 * x^83 + 36174 * x^84 - 32110 * x^85 + 35235 * x^86 - 31253 * x^87 + 34028 * x^88 - 30168 * x^89 + 32452 * x^90 - 28872 * x^91 + 30666 * x^92 - 27344 * x^93 + 28690 * x^94 - 25698 * x^95 + 26514 * x^96 - 23906 * x^97 + 24289 * x^98 - 22015 * x^99 + 21992 * x^100 - 20106 * x^101 + 19683 * x^102 - 18147 * x^103 + 17462 * x^104 - 16228 * x^105 + 15285 * x^106 - 14367 * x^107 + 13248 * x^108 - 12552 * x^109 + 11356 * x^110 - 10872 * x^111 + 9600 * x^112 - 9289 * x^113 + 8047 * x^114 - 7840 * x^115 + 6652 * x^116 - 6551 * x^117 + 5433 * x^118 - 5378 * x^119 + 4392 * x^120 - 4366 * x^121 + 3494 * x^122 - 3493 * x^123 + 2755 * x^124 - 2741 * x^125 + 2142 * x^126 - 2131 * x^127 + 1643 * x^128 - 1616 * x^129 + 1247 * x^130 - 1205 * x^131 + 925 * x^132 - 884 * x^133 + 685 * x^134 - 630 * x^135 + 497 * x^136 - 445 * x^137 + 352 * x^138 - 303 * x^139 + 251 * x^140 - 200 * x^141 + 167 * x^142 - 132 * x^143 + 112 * x^144 - 80 * x^145 + 77 * x^146 - 53 * x^147 + 45 * x^148 - 31 * x^149 + 29 * x^150 - 16 * x^151 + 16 * x^152 - 11 * x^153 + 7 * x^154 - 5 * x^155 + 5 * x^156 - 3 * x^157 + 2 * x^158 - 3 * x^159 + x^160)
Growth rate: 2.4229344350859443603937743378406416319
Perron number: yes
Pisot number: no
Salem number: no
We copy the command
dot -Tjpg -o"../graphs/8-Bugaenko.jpg" "../graphs/8-Bugaenko.graphviz"
and we get the following image:
Example 2
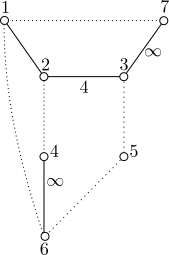
We want to check if the following subgroup of Isom H3 is arithmetic:
We encode the graph as follows:
7 3
vertices labels: 1 2 3 4 5 6 7
1 2 3
2 3 4
2 4 1
3 5 1
1 6 1
4 6 0
5 6 1
1 7 1
3 7 0
We call CoxIter with options to test arithmeticity and print the Gram matrix:
./coxiter -i ../graphs/3-testArithmeticity.coxiter -a -pgm
The output is then the following:
Reading file: ../graphs/3-testArithmeticity.coxiter
Number of vertices: 7
Dimension: 3
Vertices: 1, 2, 3, 4, 5, 6, 7
Removed vertices:
Field generated by the entries of the Gram matrix: ?
File read
Gram matrix (Mathematica):
{{ 1, -1/2, 0, 0, 0, l0m5, l0m6}, {-1/2, 1, -Sqrt[2]/2, l1m3, 0, 0, 0}, {0, -Sqrt[2]/2, 1, 0, l2m4, 0, -1}, {0, l1m3, 0, 1, 0, -1, 0}, {0, 0, l2m4, 0, 1, l4m5, 0}, {l0m5, 0, 0, -1, l4m5, 1, 0}, {l0m6, 0, -1, 0, 0, 0, 1}}
l1m3: weight of the dotted line between hyperplanes 2 and 4
l2m4: weight of the dotted line between hyperplanes 3 and 5
l0m5: weight of the dotted line between hyperplanes 1 and 6
l4m5: weight of the dotted line between hyperplanes 5 and 6
l0m6: weight of the dotted line between hyperplanes 1 and 7
Finding connected subgraphs......
Finding graphs products......
Computations......
Computation time: 0.000237657s
Information
Cocompact: no
Finite covolume: ?
Arithmetic: ? (GRAPH HAS DOTTED EDGE)
f-vector: (9, 14, 7, 1)
Number of vertices at infinity: 1
Alternating sum of the components of the f-vector: 2
Euler characteristic: 0
The group is arithmetic if and only if all the following values lie in Z:
4 * l1m3^2
4 * l2m4^2
4 * l0m5^2
4 * l4m5^2
4 * l0m6^2
2^3 * Sqrt[2] * l2m4 * l4m5 * l0m5
2^2 * Sqrt[2] * l0m6
2^3 * l1m3 * l0m5
2^6 * l1m3 * l4m5 * l2m4 * l0m6
2^5 * Sqrt[2] * l0m5 * l1m3 * l0m6
2^5 * l0m5 * l4m5 * l2m4 * l0m6
2^4 * Sqrt[2] * l2m4 * l4m5 * l1m3
With the values l1m3=-Sqrt[5]/2, l2m4=-Sqrt[2], l0m5=-Sqrt[5], l4m5=-Sqrt[5], l0m6=-Sqrt[2], we see that the group is arithmetic.

 1.8.11
1.8.11